Continued...
Other topology types
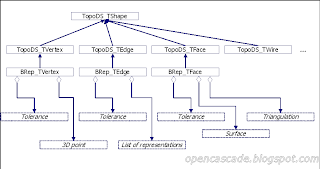
So far we considered vertex, edge, and face – those which have connection with geometry. The rest – wire, shell, solid, compsolid and compound – do not connect with geometry directly and are just containers for other topological entities:
- wire consists of edge(s);
- shell – of face(s);
- solid – of shell(s);
- compsolid – of solid(s) sharing common face(s);
- compound – of any arbitrary type (including compound).
A minor note on solids. A solid is expected to contain a single shell that describes its external boundary. If there are two or more shells, it's considered to be a solid with voids but Open CASCADE can be not too robust to work with such bodies. So beware.

Iteration over children
The are two ways to iterate over child subshapes.
1. Direct children can be retrieved using TopoDS_Iterator.
The following function will traverse through entire shape structure:
void TraverseShape (const TopoDS_Shape& theShape)
{
TopoDS_Iterator anIt (theShape);
for (; anIt.More(); anIt.Next()) {
const TopoDS_Shape& aChild = anIt.Value();
TraverseShape (aChild);
}
}
TopoDS_Iterator has two flags specifying whether to take into account location and orientation of a parent shape when extracting a child. If the location flag is on then any child is returned as if it were a standalone shape and placed exactly at its location in 3D space (i.e. the user would see an extracted edge right where it is displayed in the context of its parent wire). If the orientation flag is on, then returned child orientation will be a product of a parent and own child orientation (e.g. two reversed or forward will give forward, reversed and forward in any combination will give reversed).
If flags are off, then a child shape is returned with its own location and orientation as stored inside (recall diagram 2 in Part1). By default both flags are on.
2. Children of a particular subtype
If you want to retrieve all edges of your shape you can do the following:
TopExp_Explorer anExp (theShape, TopAbs_EDGE);
for (; anExp.More(); anExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (anExp.Current());
//do something with anEdge
}
TopExp_Explorer has an additional parameter that specifies which parent type you want to skip. For example, if you want to retrieve only floating edges (i.e. not belonging to any face – refer to Part3), you can do the following:
TopExp_Explorer aFloatingEdgeExp (theShape; TopAbs_EDGE, TopAbs_FACE);
More on location and orientation
As already described in the previous chapters, an individual location of a geometrically bounded entity (vertex, edge, face) defines a displacement relative to its underlying geometry. Location of any topology entity (regardless if it has geometric binding or not) also defines a displacement relative to its children. For instance, if a wire has a location consisting of a translation part along the {0, 0, 10} vector then it just means that all its edges are actually translated along the Z axis by 10 units.
The same works for orientation. Parent orientation affects its children orientation when extracting them from inside the shape. There is one important exception however – which is about edge orientation within a face. If you recall Part4 we discussed there that face material lies on the left of forward edge pcurves and on the right of the reversed edge pcurves. This reversed or forward orientation of an edge must be calculated *excluding* own face orientation. That is, if you need to use edge pcurves you should rather use:
TopExp_Explorer aFaceExp (myFace.Oriented (TopAbs_FORWARD), TopAbs_EDGE);
for (; aFaceExp.More(); aFaceExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (aFaceExp.Current());
}
This exception becomes understandable if you try to understand the details. Let's construct a face bottom-up:
Handle(Geom_Surface) aSurf = new Geom_Plane (gp::XOY());
//anti-clockwise circles if too look from surface normal
Handle(Geom_Curve) anExtC = new Geom_Circle (gp::XOY(), 10.);
Handle(Geom_Curve) anIntC = new Geom_Circle (gp::XOY(), 5.);
TopoDS_Edge anExtE = BRepBuilderAPI_MakeEdge (anExtC);
TopoDS_Edge anIntE = BRepBuilderAPI_MakeEdge (anExtC);
TopoDS_Wire anExtW = BRepBuilderAPI_MakeWire (anExtE);
TopoDS_Wire anIntW = BRepBuilderAPI_MakeWire (anIntE);
BRep_Builder aB;
TopoDS_Face aFace;
aB.MakeFace (aFace, aSurf, Precision::Confusion());
aB.Update (aFace, aSurf);
aB.Add (aFace, anExtW);
aB.Add (aFace, anIntW.Reversed()); //material should lie on the right of the inner wire
aFace has a forward orientation (default). Let's explore its edges and pcurves. Though we did not explicitly add them, recall (see Part 3) that for planes they can be computed on the fly:
void TraversePCurves (const TopoDS_Face& theFace)
{
TopExp_Explorer anExp (theFace, TopAbs_EDGE);
for (; anExp.More(); anExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (anExp.Current());
Standard_Real aF, aL;
Handle(Geom2d_Curve) aPCurve = BRep_Tool::CurveOnSurface (anEdge, theFace, aF, aL);
}
}
Returned pcurves will be as shown below (material will be on the left of red and on the right of blue).

Everything is correct. Now imagine we reverse the face and explore again:
TopoDS_Face aRFace = TopoDS::Face (aFace.Reversed());
TraversePCurves (aRFace);
What will we see ? All the edges will be extracted with opposite orientations and respectively their pcurves will mean that material is beyond an external wire and within an internal wire. This is clearly wrong, though original aRFace is perfectly correct. Recall Part4 that a face orientation just shows face logical orientation regarding its underlying surface. In our case aRFace will be just aFace with a normal {0, 0, -1}.
Thus, the only way out is to do the following:
TopExp_Explorer anExp (theFace.Oriented (TopAbs_FORWARD), TopAbs_EDGE);
This will ensure that edges will show orientation regarding surface (not face!) normal. I made exact same comment in Part 4. Open CASCADE algorithms take care of this particular case, make sure so do you.
Hope orientation is now also a well swallowed bit of an elephant we have been eating in this series. I think we are almost done with it. There are a few tiny bones to pick, and unless you are still hungry we will finish it in the last post to follow. Bon appetite ;-)
To be continued...
Other topology types
So far we considered vertex, edge, and face – those which have connection with geometry. The rest – wire, shell, solid, compsolid and compound – do not connect with geometry directly and are just containers for other topological entities:
- wire consists of edge(s);
- shell – of face(s);
- solid – of shell(s);
- compsolid – of solid(s) sharing common face(s);
- compound – of any arbitrary type (including compound).
A minor note on solids. A solid is expected to contain a single shell that describes its external boundary. If there are two or more shells, it's considered to be a solid with voids but Open CASCADE can be not too robust to work with such bodies. So beware.

Iteration over children
The are two ways to iterate over child subshapes.
1. Direct children can be retrieved using TopoDS_Iterator.
The following function will traverse through entire shape structure:
void TraverseShape (const TopoDS_Shape& theShape)
{
TopoDS_Iterator anIt (theShape);
for (; anIt.More(); anIt.Next()) {
const TopoDS_Shape& aChild = anIt.Value();
TraverseShape (aChild);
}
}
TopoDS_Iterator has two flags specifying whether to take into account location and orientation of a parent shape when extracting a child. If the location flag is on then any child is returned as if it were a standalone shape and placed exactly at its location in 3D space (i.e. the user would see an extracted edge right where it is displayed in the context of its parent wire). If the orientation flag is on, then returned child orientation will be a product of a parent and own child orientation (e.g. two reversed or forward will give forward, reversed and forward in any combination will give reversed).
If flags are off, then a child shape is returned with its own location and orientation as stored inside (recall diagram 2 in Part1). By default both flags are on.
2. Children of a particular subtype
If you want to retrieve all edges of your shape you can do the following:
TopExp_Explorer anExp (theShape, TopAbs_EDGE);
for (; anExp.More(); anExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (anExp.Current());
//do something with anEdge
}
TopExp_Explorer has an additional parameter that specifies which parent type you want to skip. For example, if you want to retrieve only floating edges (i.e. not belonging to any face – refer to Part3), you can do the following:
TopExp_Explorer aFloatingEdgeExp (theShape; TopAbs_EDGE, TopAbs_FACE);
More on location and orientation
As already described in the previous chapters, an individual location of a geometrically bounded entity (vertex, edge, face) defines a displacement relative to its underlying geometry. Location of any topology entity (regardless if it has geometric binding or not) also defines a displacement relative to its children. For instance, if a wire has a location consisting of a translation part along the {0, 0, 10} vector then it just means that all its edges are actually translated along the Z axis by 10 units.
The same works for orientation. Parent orientation affects its children orientation when extracting them from inside the shape. There is one important exception however – which is about edge orientation within a face. If you recall Part4 we discussed there that face material lies on the left of forward edge pcurves and on the right of the reversed edge pcurves. This reversed or forward orientation of an edge must be calculated *excluding* own face orientation. That is, if you need to use edge pcurves you should rather use:
TopExp_Explorer aFaceExp (myFace.Oriented (TopAbs_FORWARD), TopAbs_EDGE);
for (; aFaceExp.More(); aFaceExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (aFaceExp.Current());
}
This exception becomes understandable if you try to understand the details. Let's construct a face bottom-up:
Handle(Geom_Surface) aSurf = new Geom_Plane (gp::XOY());
//anti-clockwise circles if too look from surface normal
Handle(Geom_Curve) anExtC = new Geom_Circle (gp::XOY(), 10.);
Handle(Geom_Curve) anIntC = new Geom_Circle (gp::XOY(), 5.);
TopoDS_Edge anExtE = BRepBuilderAPI_MakeEdge (anExtC);
TopoDS_Edge anIntE = BRepBuilderAPI_MakeEdge (anExtC);
TopoDS_Wire anExtW = BRepBuilderAPI_MakeWire (anExtE);
TopoDS_Wire anIntW = BRepBuilderAPI_MakeWire (anIntE);
BRep_Builder aB;
TopoDS_Face aFace;
aB.MakeFace (aFace, aSurf, Precision::Confusion());
aB.Update (aFace, aSurf);
aB.Add (aFace, anExtW);
aB.Add (aFace, anIntW.Reversed()); //material should lie on the right of the inner wire
aFace has a forward orientation (default). Let's explore its edges and pcurves. Though we did not explicitly add them, recall (see Part 3) that for planes they can be computed on the fly:
void TraversePCurves (const TopoDS_Face& theFace)
{
TopExp_Explorer anExp (theFace, TopAbs_EDGE);
for (; anExp.More(); anExp.Next()) {
const TopoDS_Edge& anEdge = TopoDS::Edge (anExp.Current());
Standard_Real aF, aL;
Handle(Geom2d_Curve) aPCurve = BRep_Tool::CurveOnSurface (anEdge, theFace, aF, aL);
}
}
Returned pcurves will be as shown below (material will be on the left of red and on the right of blue).

Everything is correct. Now imagine we reverse the face and explore again:
TopoDS_Face aRFace = TopoDS::Face (aFace.Reversed());
TraversePCurves (aRFace);
What will we see ? All the edges will be extracted with opposite orientations and respectively their pcurves will mean that material is beyond an external wire and within an internal wire. This is clearly wrong, though original aRFace is perfectly correct. Recall Part4 that a face orientation just shows face logical orientation regarding its underlying surface. In our case aRFace will be just aFace with a normal {0, 0, -1}.
Thus, the only way out is to do the following:
TopExp_Explorer anExp (theFace.Oriented (TopAbs_FORWARD), TopAbs_EDGE);
This will ensure that edges will show orientation regarding surface (not face!) normal. I made exact same comment in Part 4. Open CASCADE algorithms take care of this particular case, make sure so do you.
Hope orientation is now also a well swallowed bit of an elephant we have been eating in this series. I think we are almost done with it. There are a few tiny bones to pick, and unless you are still hungry we will finish it in the last post to follow. Bon appetite ;-)
To be continued...